Методы определения расстояний
Показано, что расстояние планет от Солнца подчиняется соотношеням степенного ряда с основанием е.
Еще в 18 веке была предложена эмпирическая формула (закон Тициуса-Боде) для радиусов орбит планет солнечной системы. A = (0,4 + 0,3·2)R, где n= -, 0, 1, 2, 3..., R - радиус орбиты Земли.
В отличие от законов Кеплера это соотношение никак не следует из законов Ньютона и до сих пор не получило теоретического обоснования, хотя орбиты всех известных на сегодняшний день планет удовлетворительно описываются этой формулой. Исключение составляет лишь значение n = 3, для которого на рассчитанной орбите планеты не существует. Вместо нее был обнаружен пояс астероидов - небольших по планетным масштабам тел неправильной формы.
Гармоническая закономерность распределений временных характеристик систем приводит к гармоническим соотношениям в пространственных размерах. Проверить это можно с использованием теории размерности. Соотношение между периодами обращения планет Солнечной системы вокруг Солнца соответствует геометрической прогрессии с модулем е, т.е.
T / T = e
Учитывая закон Кеплера, по которому квадраты периодов обращения планет относятся как кубы их расстояний от Солнца:
T = [2(a)] / (GM),
Где a - среднее расстояние планеты от Солнца. М - масса Солнца, G = 6.670·10 Н·м/кг. Отсюда
T = A·(a),
Где A=2/(GM), что соответствует закону Кеплера.
Тогда из критического соотношения для периодов обращения планет (T = eT) получим критическое соотношение между средними расстояниями этих планет от Солнца
A / a = e = 1,94773...
Ниже в таблице приведены результаты расчета расстояний планет от Солнца в соответствии с установленной закономерностью. Из таблицы следует, что последовательные расстояния планет от Солнца в самом деле близки к геометрической прогрессии с модулем е (соотношение близко к удвоению расстояний, однако удвоение расстояний планет от Меркурия (ближайшей к Солнцу планеты) дает явно завышенные результаты). * Из Чайлде, 1962. ** Значение, принятое за начало отсчета. *** Среднее геометрическое расстояние пояса астероидов от Солнца.
При этом критические рубежи, соответствующие основному ритму звена развития, также обнаруживаются в структуре Солнечной системы. Если расстояние от Солнца до ближайшей к нему планеты (Меркурия) принять за единицу, можно заметить, что реализуется ряд значений, больших единицы в е, е, е, е раз (см. рис ниже). Значению расстояния в е раз большего, чем расстояние от Меркурия, соответствует положение Земли, е - пояса астероидов, е - Юпитера, е - Урана. Это показывает, что на критическом соотношении е существует орбита (между Юпитером и Сатурном), на которой может находиться планета.
Тициуса-Боде, правило
Аналитическая числовая последовательность, указывающая приблизительное расстояние планет от Солнца: если принять расстояние Земли от Солнца за 10 единиц, то расстояния остальных планет составят
R = 4 + 3 x 2N, где
| Меркурий |
|
| Венера |
0 |
| Земля |
1 |
| Марс |
2 |
| Астероиды |
3 |
| Юпитер |
4 |
| Сатурн |
5 |
| Уран |
6 |
| Нептун |
7 |
| Плутон |
8 |
Параллакс
Видимое смещение более близкого объекта на фоне значительно более далеких при перемещении наблюдателя с одного конца некоторой базы
на другой ее конец.
Если длина базы известна, то параллактический угол позволяет вычислить расстояние до объекта. При фиксированной базе сам параллактический угол служит мерой расстояния до объекта.
При измерении расстояний до объектов Солнечной системы достаточной базой служит размер Земли; при измерении расстояний до звезд - размер земной орбиты. Например, перемещение наблюдателя вследствие вращения Земли вызывает изменение суточного параллакса - угла, под которым со светила виден радиус Земли, проведенный в место наблюдения. Если светило наблюдается на горизонте, то его суточный параллакс принимает максимальное значение и называется горизонтальным параллаксом. Средний горизонтальный параллакс Солнца 8.8", Луны - 57'.
Перемещение Земли по орбите вызывает годичный параллакс (угол, под которым со светила виден радиус земной орбиты, перпендикулярный лучу зрения). У близких звезд он имеет заметное значение, хотя и не превышает 1". В старых книгах параллакс обозначали греческой буквой ; в последние годы чаще используют латинскую букву p. Если угол параллакса (p) мал и выражен в радианах, а длина перпендикулярной к направлению на объект базы составляет B, то расстояние до объекта равно
D=B/p
Если параллакс выражен в секундах дуги, то расстояние до объекта
D=(1/p)
1парсек = 206 265 (1/p) а.е.
Описанные выше параллаксы называют тригонометрическими, поскольку они основаны на измерении углов. Однако в астрономии используются и другие, косвенные методы измерения расстояний до светил. При этом найденные негеометрическим способом расстояния часто представляют в виде параллактического угла, используя формулу p = (1 пк/D). Так появились динамический, групповой, средний, спектральный и энергетический параллаксы.
|
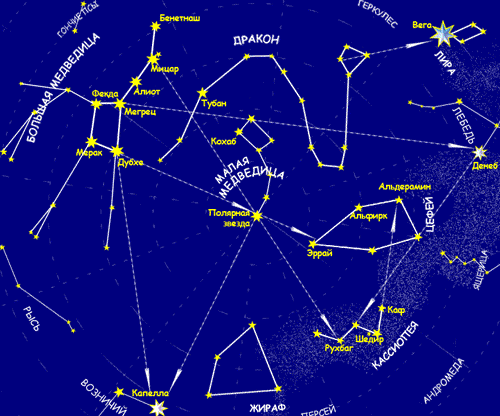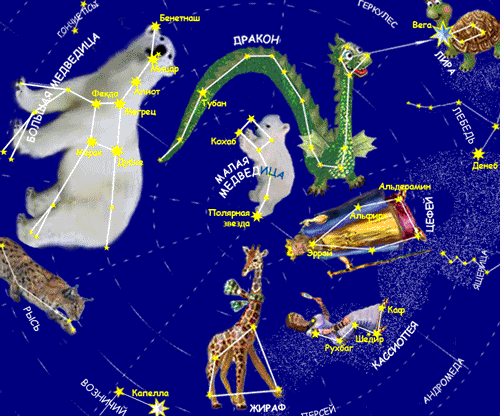От Земли к звездам
